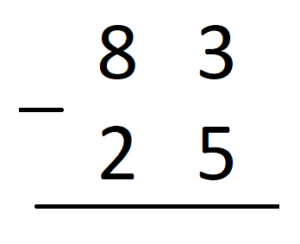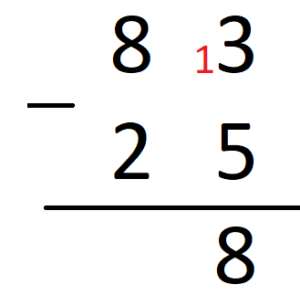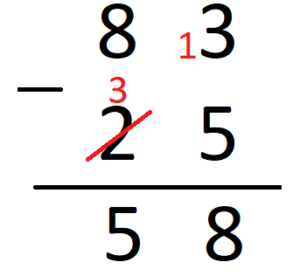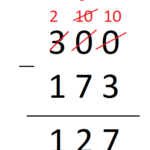Resta con llevadas (ya no se resta como antes).

Del 5 al 3 no puedo, así que voy del 5 al 13 y me llevo una. Y esa una se la doy a la decena del de abajo (del sustraendo)…¿por qué? Porque sí, porque es así. Tú haz y no preguntes.

Este sería el proceso en cuestión de la resta “de toda la vida”. La resta “de toda la vida” es como la llamamos porque es la que nos enseñaron a nosotros. La que nos enseñaron cuando lo prioritario era el qué y no el cómo, por qué y para qué.

A 83 le tengo que quitar 25. Empiezo por las unidades.“Del 5 al 3 no puedo”.

 

 

Así que voy del 5 al 13. Del 5 al 13 van 8.

 

Como fui al 13 me llevo 1.

Que se la doy al 2 del 25.

 

Así que ahora no hay 2 sino 3. Del 3 al 8 van 5.

Esa es la resta “de toda la vida”. Tú, adulto. ¿Puedes justificarla? Claro que puedes. Seguramente has dicho algo como: “sumo 10 arriba y 10 abajo y ya está”. Como la Propiedad Fundamental de la Resta dice que si al minuendo y al sustraendo le sumas o restas la misma cantidad pues la diferencia no varía. Total, que has transformado 83 en 80 y 13 y 25 en 35.

Eso es, adulto. Lo has justificado, pero lo has hecho después de la mecánica. Hace años íbamos a resultado, no al razonamiento. El razonamiento lleva un proceso que debe partir de la manipulación, pasando por la interpretación para, al final, simbolizar. Esto son teorías del aprendizaje, no son cosas de “profes de hoy”, son cosas de profes, pedagogos, psicólogos y matemáticos de hace 60 años.

Veamos, a continuación, algunas maneras de restar que parten del razonamiento y la comprensión.

EL MÉTODO DE «PREPARAR LA RESTA»

La resta en cuestión era 83 – 25. Si habéis leído los artículos anteriores recordaréis mi obsesión por dotar de significatividad a los símbolos así que digamos que “De 83 cromos que tenía, regalé 25, ¿cuántos quedan para mí?»

En esta ocasión nuestro material representará “cromos”.

1 cromo estará representado por un “cubito”.

1 paquete de 10 cromos estará representado por una barra.

1 caja de 100 cromos estará representado por una placa.

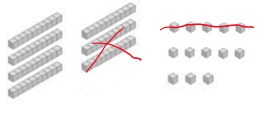
  • Así representamos los 83 cromos (8 barras y 3 cubitos):
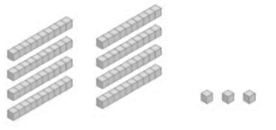
  • A 83 hay que quitarle 25. Puedo quitar 20, pero no puedo quitar 5 porque no tengo. Así que tomo una decisión. Cambiamos una de las barras por 10 cubitos:
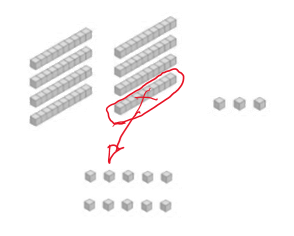
  • Ahora tenemos 7 barras (70) y 13 cubitos (13). Hemos transformado el 83 en 70 y 13.
  • Ahora a 70 y 13 le puedo quitar 20 y 5. Y me quedan 58 cromos.
  • El proceso escrito  en símbolos de lo que ha ocurrido este:

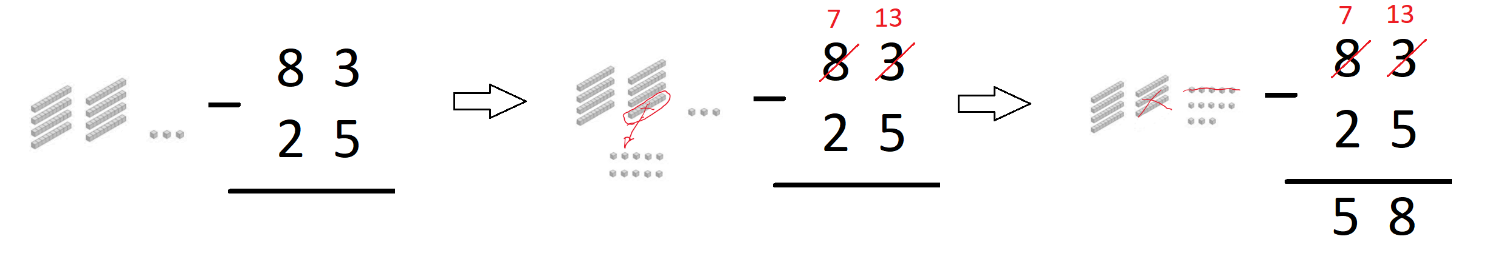
Es decir, para poder restar 83 – 25. hemos transformado el 83 en 70 y 13 y así poder quitar 20 y 5. Eso es exactamente lo que hicieron sus manos. Sé que escrito en palabras (en símbolos) puede parecer complejo pero lo que ocurre con sus manos es:

  • Represento 83. ¿Qué tengo que hacer? Quitar 25.
  • ¿Puedo quitar 20? Sí, todo va bien pero… ¡Espera! No puedo quitar 5.
  • Pues prepara el 83 para que pueda ocurrir.
  • ¡Mira!, 83 también es 70 y 13, ¿Puedes quitar 20? ¿Puedes quitar 5? ¡Hazlo!

En fase escrita se trata de que “lo que dicen los números” sea lo que hicieron las manos.

  • Tenía 8 barras y 3 cubitos (83) y tenía que quitar 2 barras y 5 cubitos (25).
  • Las 2 barras podría quitarlas pero los 5 cubitos, no.
  • Una barra se cambia por 10 cubitos. Y ahora tengo 7 barras y 13 cubitos.
  • Expresaron el 8 decenas y 3 unidades como 7 decenas y 13 unidades y así pudieron quitarle 2 decenas y 5 unidades.

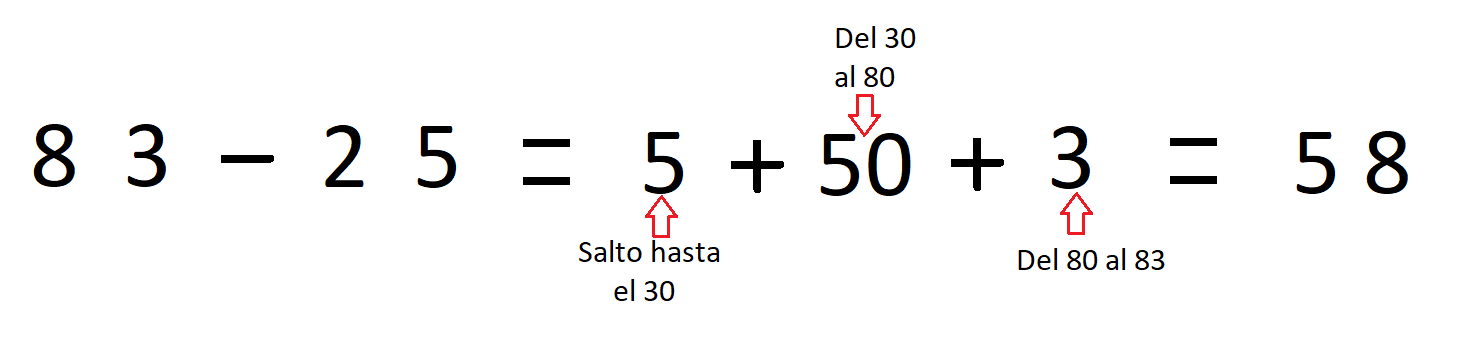
EL MÉTODO DE LOS SALTOS SEGUROS

El método de los saltos seguros se basa en lo que yo llamo “quiero ser como tú”. En este caso queremos resolver 83 – 25. O dicho de otro modo, el 25 quiere ser como el 83. ¿Cuánto le falta al 25 para ser como el 83? Vamos a dar saltos seguros que permitan a la mente recordar fácilmente en qué punto están en cada momento:

  • Hay que llegar del 25 al 83.
  • Primer salto, del 25, ¿a cuál vas? La mayoría de los niños saltan al 30. Del 25 al 30 van 5.
  • Ya estás en el 30. ¿A cuál vas ahora? Al 80. ¿Cuántos van? Van 50.
  • Ya estás en el 80. ¿A cuál vas ahora? Al 83. ¿Cuántos van? Van 3.
  • Diste un salto de 5 y uno de 50 y uno de 3. En total, diste un triple salto de 58.

Prueba con una de esas “rollo”. Tipo 300 – 173. Estas les suelen dar a los niños más quebraderos de cabeza pero, en realidad, con el método de los saltos seguros, seguro que le resulta más fácil. Mira:

EL MÉTODO DE LAS RESTAS PARCIALES

Como su propio nombre indica iremos restando por partes, según te convenga o interese. Resta cada vez lo que sea adecuado para tu mente. Si a 83 le puedes quitar 25 de golpe es un método bueno para ti, ¡hazlo! Pero si yo no puedo, entonces no es bueno para mí y tengo que buscar mi camino.

Por ejemplo:

  • En 83 – 25. Para mí es fácil quitar 20, me quedan 63.
  • Ahora tengo que quitar 5. Pues quito 3, me quedan 60. Y quito 2 más, me queda 58.

En el caso de la resta complicadilla de antes (300 -173). También funciona, mira:

  • En 300 – 173 es fácil quitar 100, me quedan 200.
  • A 200 le quito 70, eso es fácil. Me queda 130.
  • A 130 le quito 3 y me queda 127.

 

EL MÉTODO DE LAS RESTAS EQUIVALENTES

Comencé el artículo con el “método de toda la vida” que no es otra cosa que transformar una operación en otra. El problema es que la transformación que se hacía era un poco extraña. Vamos a simplificarlo un poco pero para ello nos vamos a aquello que de manera recurrente cuento en el blog. ¡La verticalidad!

Los niños en 3 años juegan a “ser igual y ser no igual”, a “ser igual y ser diferente”. Vamos a jugar a eso. Historieta rápida:

Paco y Pepe son gemelos, son idénticos. Siempre van igual vestidos. Están obsesionados con ir siempre igual.

Estos son Paco y Pepe:

 

Los pequeños de 3 años no tardan ni 1 segundo en darse cuenta de que al pobre Pepe le falta la nariz.

Está bien, se la pondremos.

 

Ya son iguales, idénticos. A Pepe solo le faltaba la nariz para ser igual que Paco.

 

 

¡Paco y Pepe se van de boda con sus padres! Siempre van muy elegantes. Se han puesto una pajarita de lo más bonita. Si se la pone Paco, se la pone Pepe. Así no habrá diferencia:

Paco y Pepe no se conforman con una simple pajarita. Como es un día muy soleado hay que cubrirse la cabeza (además ellos tienen poquito pelo). Así que se han puesto un sombrerito para protegerse.

 

 

Paco y Pepe están elegantísimos. Los dos iguales. Lo que tiene Paco lo tiene Pepe y lo que tiene Pepe lo tiene Paco pero…

 

¡Qué calor! Pepe no ha podido resistir el calor y se ha quitado la pajarita.

 

 

En pocos segundos tendrás a los niños gritando en clase: ¡Quítale la pajarita a Paco! O ¡Ponle la pajarita a Pepe!

 

La cosa es que sean iguales.

Total, que Paco se ha quitado la pajarita. Si le quito la pajarita a Pepe y le quito la pajarita a Paco, ¡la diferencia no varía!

Contada la historieta de Paco y Pepe volvamos a la resta esa molesta, a esa que les cuesta. Esas que tienen un montón de ceros en el minuendo, 300 – 173.

Si a 300 le hago algo y le hago lo mismo a 173, la diferencia no varía. Mira, atento:

  • Si la hiciéramos con el método de preparar la resta. Pasaría esto:

Estaría estupendo. De hecho, es mi método favorito pero muchos profes y padres dicen: ¡Qué horror tanto tachar y tachar en el cuaderno! Tengo que decir que, en este caso, el tachado denota razonamiento (de hecho, se sabe que los apuntes de Einstein estaban llenitos de tachones), pero bueno… ¡Volvamos a ver qué tienen que ver Paco y Pepe en todo esto:

Si a Paco le quito la pajarita, entonces se la quito a Pepe y, así, la diferencia no varía. Si lo que le quite a 300 se lo quito también a 173, entonces la diferencia no varía.

¡Para qué me voy a complicar más de la cuenta, le quito 1 al de arriba y 1 al de abajo y la diferencia no varía! Así que la operación quedaría así. Prueba a resolverla, ya verás como ya no es una de esas temidas restas con llevadas. ¡Hemos hecho desaparecer las llevadas! ¡Magiaaaaa! Nooooo, matemáticas. La magia está llena de trucos y los TRUCOS EN MATES NO EXISTEN.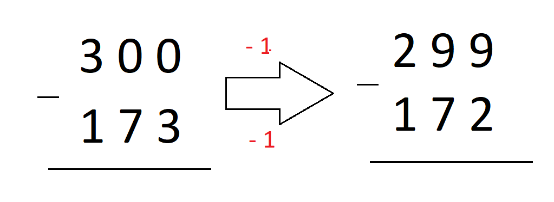¡Da igual cómo se reste! Hay tantas maneras de restar como cabecitas en tu clase.

Si les llevas por un único camino es porque les llevas por tu camino, no por el suyo.

Déjales que resten como quieran. Quitando, poniendo, dando saltos… ¡Como si quieren restar en Excel!

No pienses por él. Él puede solo, en serio. Es solo cuestión de darles los materiales adecuados, hacerles las preguntas idóneas para desencadenar el aprendizaje y que se convenzan de que descubren y conquistan por sí mismos.

 

Para leer el articulo original pincha aquí.

Profe Bernabeu.