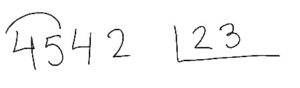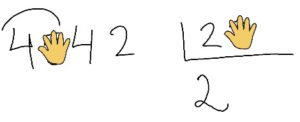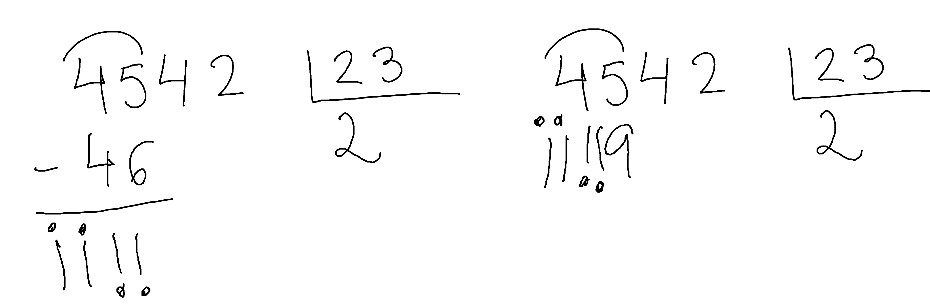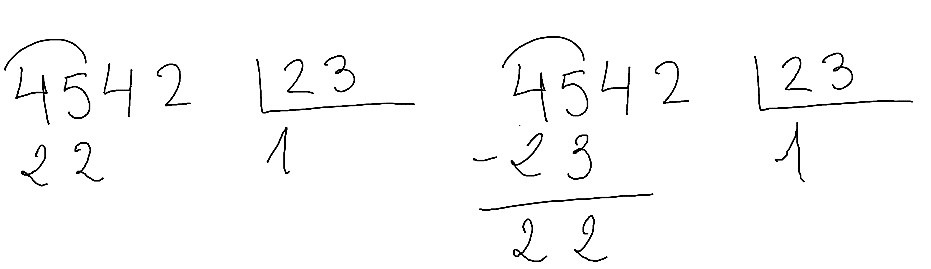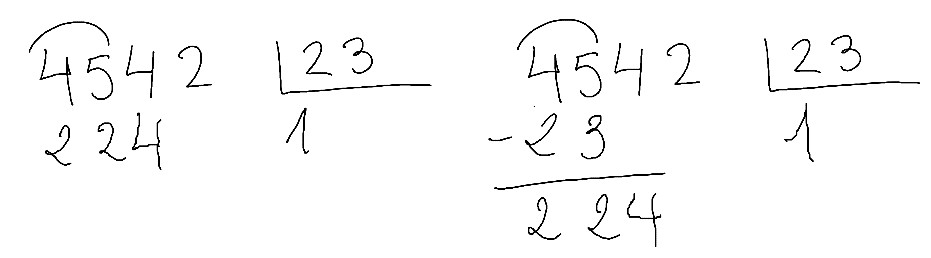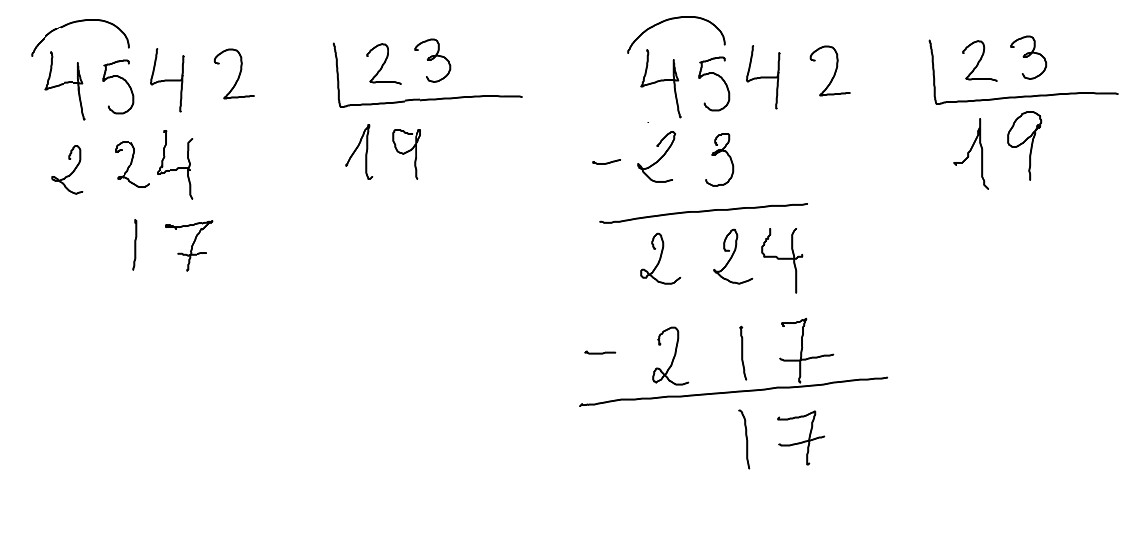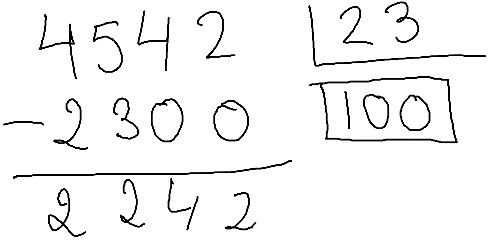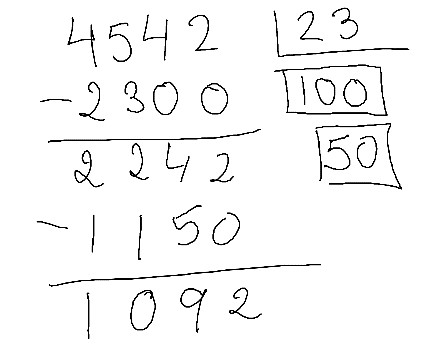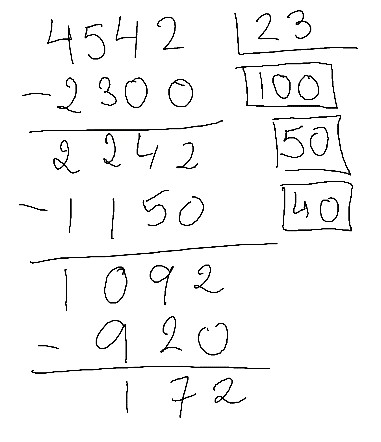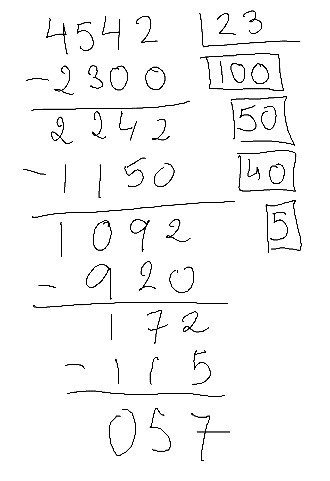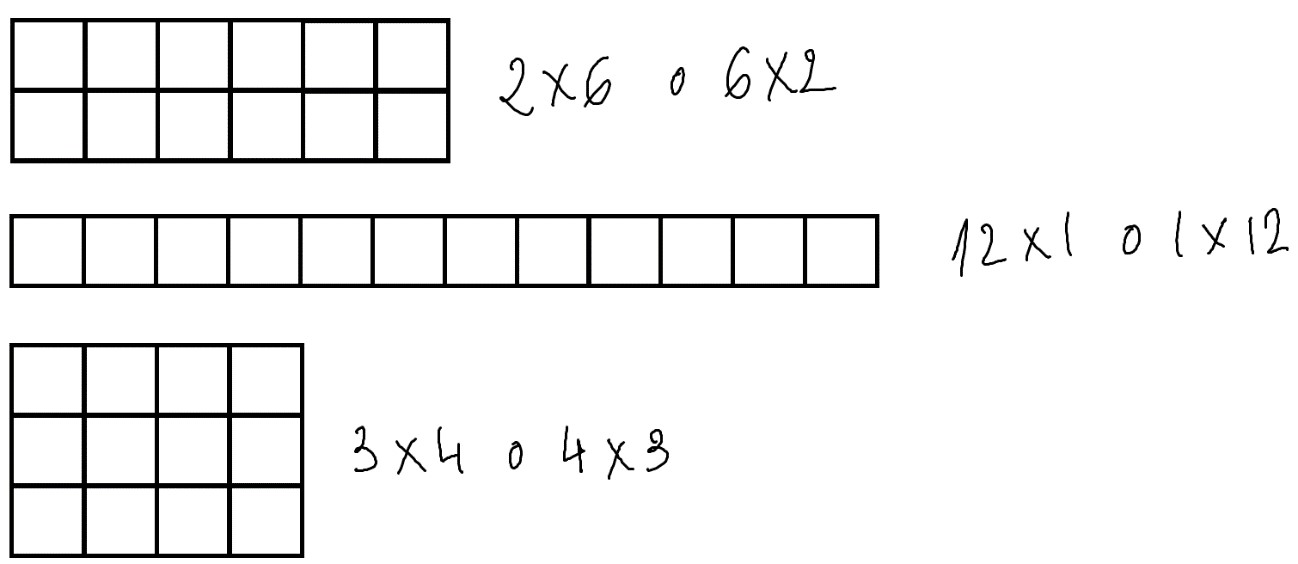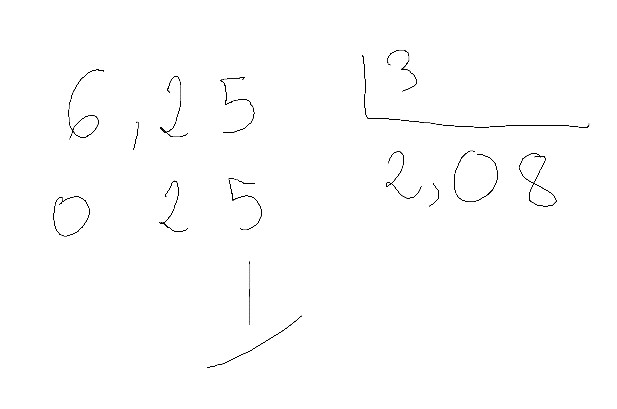Sin duda, el caballo de batalla en primaria es la división de dos cifras. Es el que caballo de batalla en España, que es de los pocos países que seguimos ahí con el tema de las divisiones por dos cifras erre que erre (y las raíces).
¡Que tienen que saber dividiiiiir! ¡Valeeeeeee! ¿Tú sabeeeeeees o tiras de móvil?
Bueno, da igual. Si hay que hacerlo se hace, pero apoyémonos en lo que saben porque el método de “tapa y tapa” es un pelín flojo. ¿No conoces el famoso método de “tapa y tapa”?
El método de tapa y tapa
Es ese método en el que se tapa una cifra del divisor y una de la parte del dividendo que queda recogido en la coronita.
Por ejemplo, si la división es esta:
Dicen… Tapo el 3 y tapo el 5. Y 4 entre 2 es 2. Ahora a ver cuanto sobra… ¡y listo!
Pero claro. Ir a lo mecánico, a la falta de estimación, a no mirar la cantidad sino la cifra, a no tener un mínimo de sentido numérico nos lleva a situaciones como esta (lo muestro para los que ponen la resta y para los que no):
Básicamente el problema es que 23 x 2 es 46 y solo había 45 por dividir. ¿¿¿En serio era tan difícil darse cuenta de que el 2 no vale. O como decimos en clase: “no cabe”???
Total, que el 1 “sí cabe” y decimos algo como 1 x 3 son 3 hasta el 5 van 2. 1 por 2 son 2 hasta el 4 van 2:
Luego bajan la cifra siguiente y, entonces, dividen 224 entre 23.
Si hacen el “tapa y tapa” daría 11, pero todo el mundo sabe que en el cociente solo de una cifra en una cifra. ¿Por qué? Porque sí, porque es el método de “tapa y tapa” y es así (¿se nota que no es mi método favorito?)…
Total, que si no es el 11, ni el 10. Seguramente sea el 9 el que nos vale. Pero nos encontramos con una dificultad generalizada en los niños de 4.ºEP cuando están empezando:
La dificultad (en caso de hacerlo sin resta es esta): 9 x 3 son 27, vamos hasta el 34… ¿¿¿¿Y por qué al 34???? Esto les cuesta un montón (les cuesta menos si trabajaron por descomposición cuando estaban en 2.ºEP pero, aún así, les cuesta. Les cuesta ver que el 224 se puede ver como 190 y 34, que es lo que ocurre cuando vamos al 34). Si le metes la resta aligeras un poquito la dificultad, pero no mucho.
En fin, que seguimos. No sin dificultad porque si aplico el “tapo y tapo” diríamos que 17 entre 2 son 8 pero al probar veríamos que “no cabe” así que serán 7:
Bueno, pues este es el método de “tapa y tapa”. Que podría llamarse también el método “de toda la vida”.
El método de las restas parciales
Al método de las restas parciales yo lo llamo: “A mi ritmo”.
Para dividir con este método tenemos que dominar el valor de posición. Es decir, la cantidad en tooooooda su extensión… Nada de ver el dividendo cifra a cifra. Lo veremos enterito. Y el divisor también enterito. Sin “tapa y tapa” Vamos allá. Cada uno a su ritmo:
¿Os acordáis de lo de “hacer grupos”? Pues eso haremos, pero cada uno a su ritmo. Por ejemplo, así:
Tengo 4542 tomates y quiero agruparlos de 23 en 23.
¿Podría hacer 1 grupo? Claroooooooooooooo
¿Podría hacer 100 grupos? Claroooooooooooo
¿1000 grupos? Noooooooooooo
Ok, primera aproximación conseguida.
Entonces puedo hacer 100 (100 x 23 es muuuy fácil, son 2300)
¿Y puedo hacer 200? (Si sé cuánto es 100 x 23, también sé 200 x 23, son 4600). Ups, no puedo hacer 200 grupos. Vale, haré 100 y veré qué me queda después por agrupar:
Ok, ahora me quedan 2242 tomates por agrupar de 23 en 23. ¿Puedo hacer otro grupo de 100? Nooooo, 100 x 23 es 2300 y ya solo quedan 2242 tomates. Pues llega el momento de estimar.
Suele ser sencillo ir a doble y mitades. Si no puedo hacer grupos de 100, ¿puedo hacer grupos de 50? 100 x 23 es 2300, pues 50 x 23 es la mitad. 1150. ¡Adelante con el 50!
Ahora tengo que agrupar 1092 tomates de 23 en 23. 10 grupos seguro que puedo porque 10 x 23 es 230. ¿Podré 20? ¡Es el doble! 460. ¿Y podré 40? ¡Es el doble! 920. ¡Adelante con el 40!
Ahora tengo que agrupar 172 tomates de 23 en 23. ¿Puedo 10? Ups, no. Porque 10 x 23 son 230. Voy a la mitad. ¿Puedo 5? La mitad de 230 es 115. Así que, ¡sí puedo!
¡Jolín, esto no se acaba nunca! Bueno, cada uno a su ritmo, era el trato. Dividir comprendiendo y sabiendo qué quiere decir cada número.
Total, que quedan 57 tomates por agrupar de 23 en 23. ¿Es posible? 1 grupo, seguro. 2 grupos también. 3 grupos, no.
Pues mira, ahora suma los cocientes parciales y verás que el resultado es 197 y el resto es 11.
¿Es más largo? Sí ¿Cada niño elige su camino? Sí
¿Queréis saber qué método elegiría yo para hacer divisiones “tediosas” como la de arriba? LA CALCULADORA como la mayoría de los países esos donde se les dan tan bien las mates (Singapur, China, Corea…)
En fin, nuestro currículo lo pide. Pide que los niños dividan entre varias cifras (algunas comunidades incluso marcan un tiempo para resolverlas). Pues nada, si lo hacen que al menos sepan lo que hacen.
El método de los rectángulos
Todo producto se puede representar con rectángulos. Por ejemplo:
Busca todos los rectángulos del 12:
Ahora fíjate qué conclusiones podemos extraer:
- 12 : 6 = 2 Tenemos 12 cuadraditos que utilizar. Si un lado es 6, ¿cuánto es el otro?
- 12 : 2 = 6 Tenemos 12 cuadraditos que utilizar. Si un lado es 2, ¿cuál es el otro?
- 12 : 4 = 3 Tenemos 12 cuadraditos que utilizar. Si un lado es 4, ¿cuál es el otro?
- 12 : 3 = 4 Tenemos 12 cuadraditos que utilizar. Si un lado es 3, ¿cuál es el otro?
Vamos a cantidades mayores a ver si funciona. Mira cómo resolvemos por rectángulos, 784 : 34
Tenemos 784 que utilizar. Si un lado es 34, ¿cuánto cale el otro?. Vamos pasito a paso
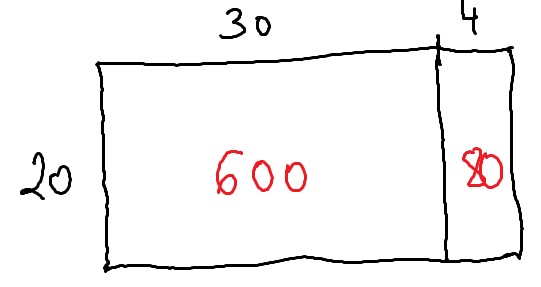
Digamos que esto es 34 (30 y 4):
¿Cómo tiene que ser el rectángulo de alto para conseguir los 784?
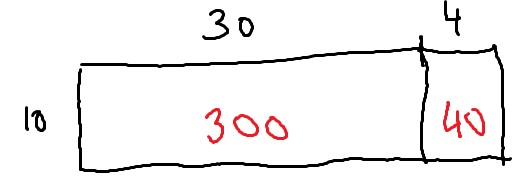
Si pusiéramos 10 ocurriría esto:
Habríamos conseguido el valor 340 (300 + 40) que está demasiado lejos del 784. Por estimación y un mínimo de cálculo mental podríamos averiguar que podría medir 20 en lugar de 10 y así nos acercaríamos más y de manera más rápida, mira:
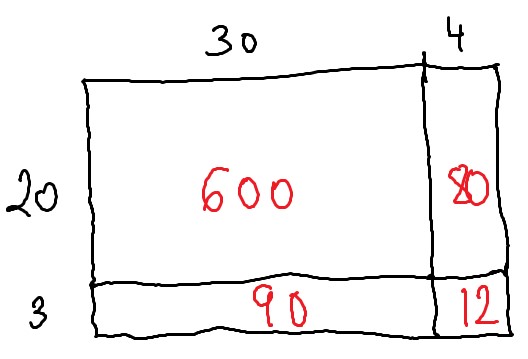
Si el lado que queremos averiguar valiera 20 conseguiríamos un rectángulo de 680. ¡Pero queríamos 784! Aún faltan 104. Veamos como conseguir lo que falta:
Es sencillo estimar que si añadiera 3 más de alto conseguiría otras nuevas zonas en el rectángulo con el valor 90 y 12 (que es 102)… ¡Estamos súper cerca!
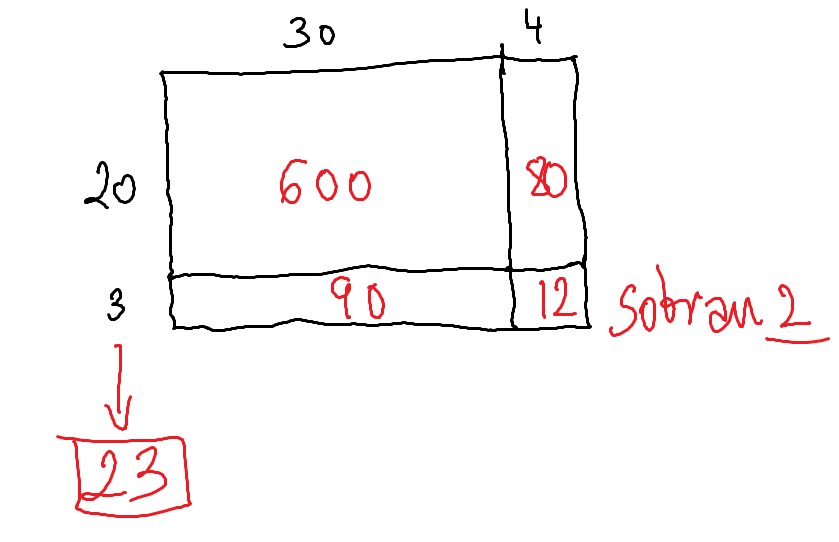
Así que podemos decir que con 784, si sé que un lado del rectángulo vale 34, el otro vale 23 (y sobran 2).
O lo que es lo mismo, 784 : 34 = 23 r2
Este es otro método más. Hay gente (adultos, generalmente) que ven complejo este método. Este método requiere de un mínimo de cálculo mental por estimación. Si previamente se ha trabajado la multiplicación por rectángulos este método les resulta sencillo. Mira, lo de la multi por rectángulos no es más que esto.
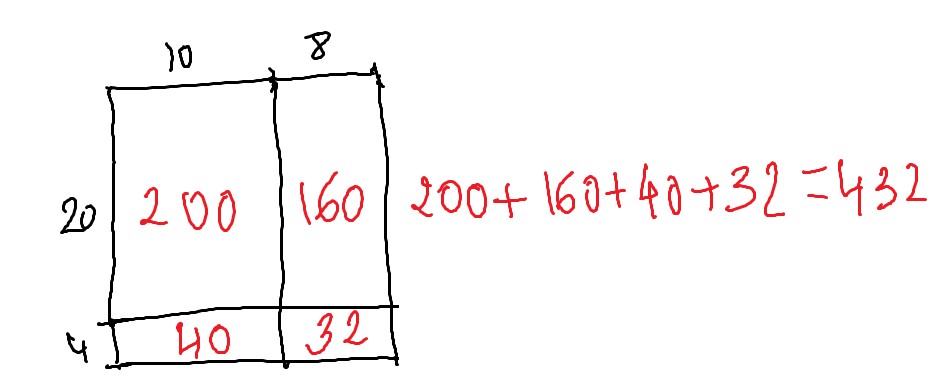
18 x 24 Tenemos que dibujar un rectángulo de 18 x 24 (10 y 8 por 20 y 4).
Del mismo modo podemos decir que 432 : 18 = 24 y que 432 : 24 = 18
El resto de las divisiones con decimales
Problema generalizado en 5.º y 6.º EP (y en secundaria también).
Resulta que hacen una división de esas con decimales y les queda resto. Van los pobrecillos a hacer la prueba y no les da… Por ejemplo:
Y entonces va el niño y dice: ¿Me la corriges, profe?
Y tú, dices: ¡Haz la prueba!
Y él hace: 2,08 x 3 + 1. Y cuando calcula eso le da 7,24 y el pobre piensa que está mal la división. ¿Sabéis por qué?
Porque no supo que el resto de esa división no es 1 sino 0,01.
¡PORQUE MUCHOS ALUMNOS NO DOMINAN EL UNO! Y esto me lleva a acabar el artículo diciendo:
¿Domina tu alumno el UNO? Porque si no es así, no te molestes en que elija un método de división.
Para leer el articulo original pincha aquí
Profe Bernabeu