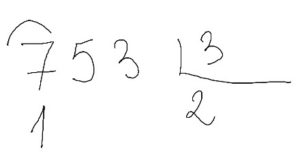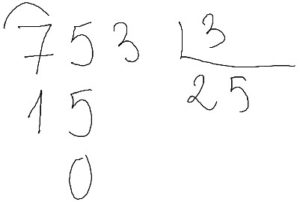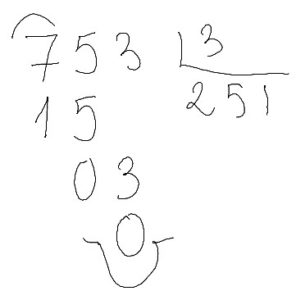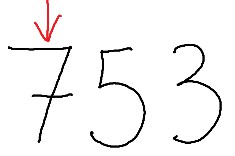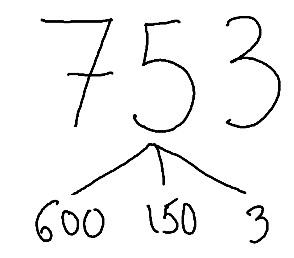Después de “Ya no se resta como antes” llega “Ya no se divide como antes”.
Bueno, vamos a hacer una pequeña apreciación sobre los títulos de aquella y de esta entrada para no llevarme más tirones de orejas de profes y papis:
- Donde dije “Ya no se resta como antes” diremos “Ya no SOLO se resta como antes”
- Donde digo “Ya no se divide como antes” diremos “Ya no SOLO se divide como antes”.
DIVIDIR ES REPARTIR. ¿SIEMPRE?
Dividir es repartir. Esto es lo primero que le decimos en clase en muchas ocasiones a los niños. ¿Es esto cierto? ¿Es esto cierto siempre? ¿Qué consecuencias tiene que el niño asocie siempre repartir con dividir? Pues mira, para algunos no tiene consecuencias, pero para otros tiene consecuencias “fatales” porque en lugar de comprender una determinada situación-problema que te lleve a tomar decisiones para encontrar el camino de la resolución se limitan a buscar la palabra clave.
Las palabras clave están muy extendidas en las aulas. De hecho, en muchas hay carteles recordando algo así:
SUMAR: Juntar
RESTAR: “¿Cuánto queda?” “¿Cuánto falta?” “¿Cuánto sobra?” “más que” “menos que”
MULTIPLICAR: “veces”, “repetido”
DIVIDIR: “Repartir”
Por tanto, casi sin darnos cuenta, propiciamos que los niños busquen palabras clave en lugar de ir a la comprensión de la situación y pasan cosas así:
Mirad chicos, hoy, por vuestro buen comportamiento, os voy a repartir 2 pimientos a cada uno de los 24 alumnos (repartir caramelos ya no está bien visto). ¿Cuántos pimientos repartiré?
¡Ajá! ¡Ahí está repartir! Y hay un 24 y un 2 así que habrá que hacer 24 : 2. ¡Eso está chupado!
Mejor no asociar palabras. Mejor asociar situaciones a acciones:
- ¿Quién participa en esta historia, en esta situación? Los niños de la clase.
- ¿Cuántos son? 24
- ¿Qué les va a repartir el profe? Pimientos
- ¿Cuántos a Juan? 2 pimientos. ¿Cuántos a Arantxa? 2 pimientos. ¿Cuántos a Lucía? 2 pimientos…
- ¿Cuántas veces 2 pimientos? 24. ¿24 qué? 24 veces. ¿24 veces qué? 24 veces 2 (24 x 2).
El germen de la división (como de todo) está en infantil.
Las tareas de reparto, de hacer grupos iguales, de asociar, de aplicar el principio de correspondencia, de clasificar, etc, son tareas propias de infantil que esconden detrás lo que será más adelante el concepto de división (y de otros muchos).
Se trata de proponer sencillas tareas que incluyan un conflicto. Un conflicto cognitivo que haga que algo chirríe en la cabecita del niño y, por pura justicia, reaccionen, tomen decisiones y empiecen a construir.
En el juego de hoy vamos a colocar pelotas dentro de los aros:
Imaginad que queda esa representación. No os quepa duda de que tendréis a prácticamente a toda la clase quejándose amargamente (por supuesto a gritos). ¿Sabéis por qué? ¡Por los patrones! (sé que soy pesadito con los patrones). Entonces empiezan una serie de preguntas por parte del profe que tienen como intención que se calmen, que dejen de gritar. No a base de “¡que os calléis!” sino a base de “¿pero que os paaaaaaaasa?” Porque lo que queremos es que de la boca del niño empiecen a salir cosas como “grupos iguales”, “no es justo”, “así no vale”(aunque en el fondo claro que vale. En cursos posteriores verán en esa representación cosas como 2 x 4 + 3 y entenderán desde el contexto eso de la jerarquía de las operaciones).
Total, que esa representación “arreglada” para que los niños dejen de pegar voces (4 bolas en cada aro, por ejemplo) se puede interpretar matemáticamente de muchas maneras. Y cuando estamos trabajando la división no deberíamos olvidarnos de que esta va siempre ligada a la multiplicación pudiendo interpretar esto de muchas formas:
- 3 aros con 4 pelotas en cada aro es 3 x 4
- 4 pelotas en cada uno de los 3 aros es 4 x 3
- 12 pelotas se han repartido a partes iguales en tres aros es 12 : 3
- 12 pelotas en grupos de 4 pelotas es 12 : 4
Así que, como siempre, partiremos de la manipulación (fase concreta), pasaremos a la interpretación de lo manipulado (fase icónica) y luego a la interpretación del símbolo (fase abstracta).
Métodos de dividir (entre una cifra)
Así divide así, así. Así divide así, así. Así divide así, así. Así divide que yo lo vi (ya no te sacarás la musiquilla de la cabeza).
No hay métodos mejores que otros para dividir. Cada uno debería poder escoger el más adecuado para él. Pero para poder escoger hay que comprender qué quiere decir cada símbolo de los que está escrito. Eso debería ser fundamental si pretendemos que el niño comprenda. Si solo queremos autómatas que siguen algoritmos sin plantearse qué, por qué y para qué entonces, dejad de leer ya.
Método de “buscar en la tabla”
7 5 3 : 3
Este es el método probablemente que aprendimos la mayoría cuando éramos niños. Es el típico de “busco en la tabla del 3 un número que multiplicado por 3 me dé 7 (o cerca)”. Y el niño dice 3 x 2 es 6 hasta el 7 va 1 (la coronita encima del siete es otro clásico).
Bajo la cifra siguiente y busco en la tabla del 3 un número que multiplicado por 3 me dé 15 (o cerca). Y el niño dice, 5 x 3 es 15 hasta el 15 van 0.
Bajo la cifra siguiente y busco en la tabla del 3 un número que multiplicado por 3 me dé 3. ¡Chupado! El 1. Y el niño dice, 1 x 3 es 3 hasta el 3 van 0. Y como no me queda nada por bajar se acabó la división.
Este método lo podéis encontrar también con las restas escritas. ¿Qué restas? Cuando el niño dijo 2 x 3 es 6 hasta el 7 va 1 podría haber escrito el 6 debajo del 7 y restarlo.
Vale, es cierto que sirve para resolver la división este método. Pero, ¿sabe el niño qué está haciendo? ¿Sabe por qué busca en la tabla? ¿Sabe por qué no puede pasarse? ¿Sabe que cuando divide el 7 entre 3 en realidad está dividiendo 700 entre 3? ¿Sabe qué es eso de “bajo la cifra siguiente”?
¡No quiero que comprenda solo que haga divisiones! Pues entonces, no tengo más que decir. Así está bien. También puedes dejar de leer aquí la entrada.
Método de descomposición
Para este es necesario que el niño tenga dominio sobre el significado de cada cifra de un número. Esto se trabaja desde que están en 1.ºEP y trabajan la decena. Y sí, sin ánimo de polemizar con los métodos de tres siglas… ¡Trabajar la decena antes de 1.ºEP es un sinsentido!
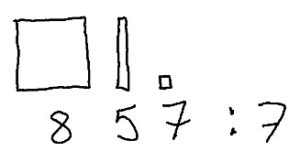
Es decir, a la pregunta: ¿Qué pone aquí?
El niño debería decir sin dudar que pone 700. Puedes utilizar todo tipo de técnicas para que el niño domine esto. Por ejemplo, la lectura deeeeeespacito: “seeeeeeeteeeeeeeeciiiiiiiiiennnnnnttttttooooossss treinta y cinco”
Pero si ha manipulado previamente con bloques de base diez tendrá la imagen mental en su cabeza de que 7 placas representa 700.
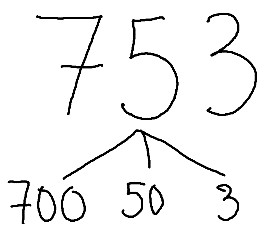
Total, que el niño debería poder ver el 753 así:
Ahora tiene que dividir 700 entre 3. 50 entre 3 y 3 entre 3.
¡Es que 700 entre 3 no es nada fácil! ¿Y qué sería fácil para ti? Y el niño dice sin dudar, 600 sería fácil. Vale, genial. Pero es que tienes 700 y tarda poco en tomar la decisión de descomponer el 753 así:
Elegida la descomposición adecuada ya es tan simple como dividir cada parte entre 3. Mira así:
¿Os habéis fijado que he metido cada resultado parcial en un recuadro? Son tarjetas de composición (cositas de María Montessori). Se acoplan unas otras así: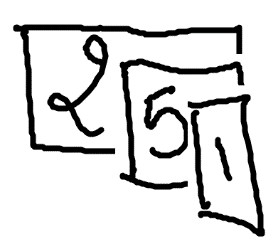
Método de hacer grupos
El método de hacer grupos es muy adecuado cuando se ha manipulado y hemos podido generar la imagen mental. Lo que tiene de particular es que desarrollan el cálculo mental por visualización de grupos.
Decíamos al principio que no siempre dividir es repartir. ¿Y si hablamos de hacer grupos iguales?
A la placa la llamaremos 100, a la barra la llamaremos 10 y al cubito lo llamaremos 1.
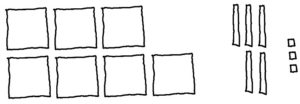
Entonces, para representar 753 haríamos esto:
Y ahora haríamos preguntas en términos de grupos:
Con 7 placas, ¿puedes hacer grupos de 3? Sí. ¿Cuántos? 2 ¿Sobra algo? 1 placa.
¿Qué puedo hacer con la placa que sobre? Cambiarla por 10 barras. ¿Cuántas barras hay ahora? 15. ¿Puedes hacer grupos de 3 con ellas? Sí. ¿Cuántos? 5 ¿Sobra algo? No.
Nos fijamos en los cubitos. ¿Puedes hacer grupos de 3? Sí. ¿Cuántos? 1 ¿Sobra algo? No.
Mira lo escrito en rojo. 753 : 3 = 2 5 1 y no sobra nada.
Hacer grupos favorece la imagen mental
Este método, como decíamos favorece la resolución desde imagen mental. Mira verás:
¿Grupos de 3 con las 3 placas? 1
¿Grupos de 3 con las 4 barras? 1 y sobra una barra que cambio por 10 cubitos.
Ahora tienes 15 cubitos. ¿Grupos de 3 con 15 cubitos? 5
Resultado: 1 1 5 y no sobra nada.
¿Un poco más difícil?
¿Grupos de 7 con 8 placas? 1 y sobra una placa que cambio por 10 barras.
¿Grupos de 7 con 15 barras? 2 y sobra una barra que cambio por 10 cubos.
Ahora tienes 17 cubitos. ¿Grupos de 7 con 17 cubitos? 2 y sobran 3 cubitos.
Resultado: 1 2 2 r3
Entre 1 cifra es demasiado fácil. ¿Qué pasa al dividir entre dos cifras o más?
Eso lo veremos en el episodio II. Pero, para ir abriendo boca, os dejo la foto de una división hecha por Lucas con su pijama de Pikachu (4.ºEP) apoyándose en el método de los restos parciales y eligiendo su camino:
Para leer el articulo original pincha aquí
Profe Bernabeu