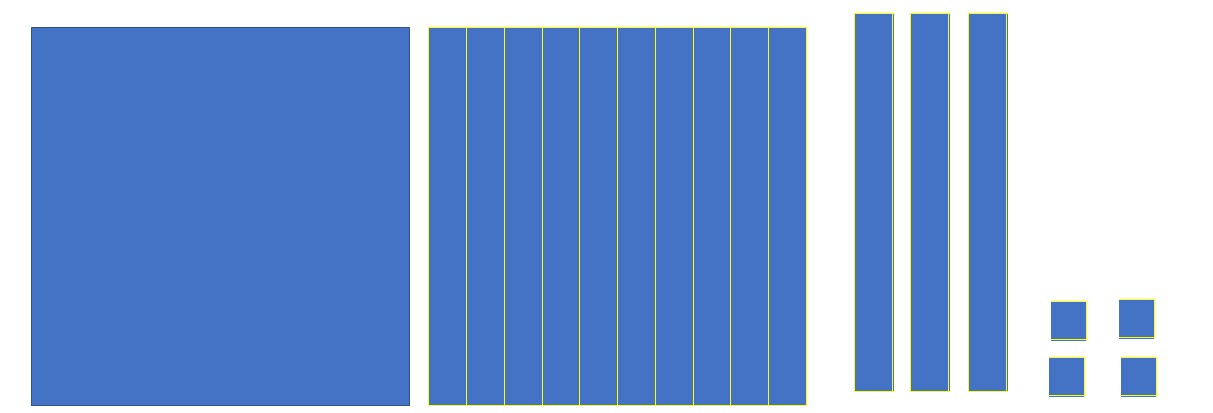
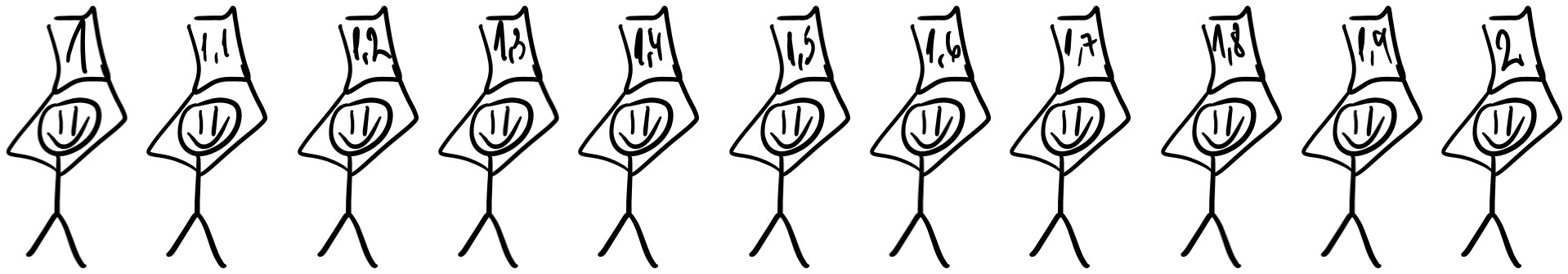Vimos en la entrada anterior que si mirábamos el uno por dentro, veíamos rápidamente las diez barras que tiene dentro:
Pues bien, si agudizas un poco más la vista verás que cada una de las barras también está dividida en 10 partes. Mira:
Si la placa entera representa UNO y la barra es eso a lo que llamar décima, vemos rápidamente dos cosas:
- Al cuadradito pequeño lo podemos llamar centésima (porque hay 100 de esas en la unidad).
- También podemos ver en cada décima hay 10 cuadraditos. Es decir, que la décima parte de la décima es eso a lo que llamar centésima.
Leyendo números decimales. A las cosas por su nombre
Decíamos en el artículo anterior que es importante que llamemos a las cosas por su nombre, que nos puede ayudar a la comprensión. A mí siempre me ha gustado apoyarme en muros de descomposición. Gracias a los muros podemos, de un golpe de vista nombrar al número decimal de muchas formas (y, obviamente, será también aplicable al cambio de unidades). Como siempre, toda fase simbólica ha de ser consecuencia de las fases concreta y pictórica.
El proceso es el siguiente:
- Representamos la cantidad con materiales.
- Enunciamos la cantidad llamando a las cosas por su nombre.
- Planteamos un pequeño reto. Un «¿Y si…?» Un «imagina que…».
Representamos la cantidad 2,34
Llamamos a las cosas por su nombre: 2 unidades, 3 décimas y 4 centésimas
Pero, ¿y si…? ¿Y si tienes que representar 2,34 pero solo tienes una placa cuadrada?
Entonces el niño no tarda mucho en decir que si solo tiene una placa tendrá que representar la otra con diez barras (por ejemplo) y representará algo así:
Y dirá cosas como 1 unidad, 13 décimas y 4 centésimas y verá que equivale a lo mismo y que, a veces, es necesario cambiar para poder ejecutar acciones.
El muro de descomposición
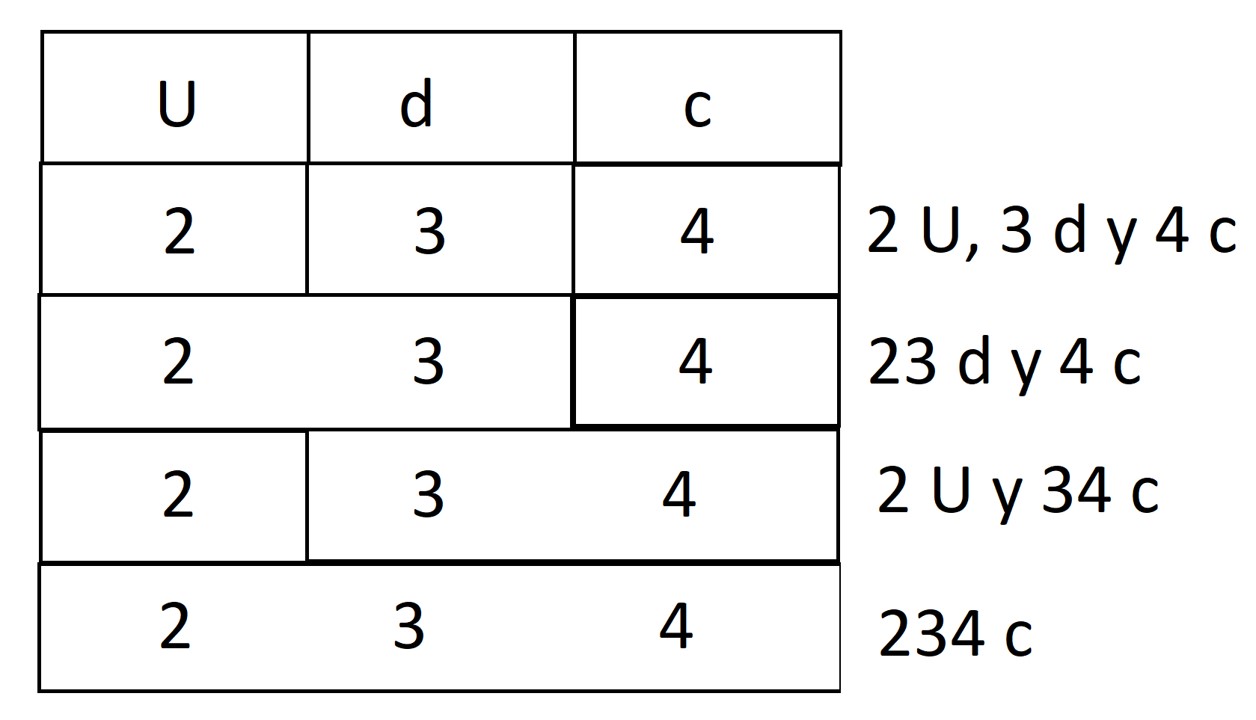
Llegados al punto en el que realizan cambios sin problema y que enuncian la cantidad representada con soltura pueden trabajar en un muro de descomposición de este tipo:
Este muro es consecuencia de instrucciones de este tipo:
- Representa con tus materiales 2 unidades, 3 décimas y 4 centésimas.
- ¿Cómo lo representarías sin utilizar placas? 23 décimas y 4 centésimas.
- ¿Y si pudieras utilizar placas pero no barras? 2 unidades y 34 centésimas.
- ¿Y si solo utilizas centésimas? 234 centésimas.
¿Tiene siguiente un número decimal?
De acuerdo. Hemos visto el uno por dentro. Hemos visto que tiene décimas y centésimas. Si hubiéramos ajustado más el microscopio habríamos visto milésimas y diezmilésimas y muchas partes más y más pequeñas. Y aquí es donde viene otra dificultad en el trabajo con los decimales. ¿Qué número va después de…?
Dinámica que suelo hacer en clase y les gusta (y a mí también):
- Elijo a dos niños. A uno le doy un cartel con un 1 y a otro un cartel con un 2. Les pido que se pongan a cierta distancia.
- A continuación, pregunto a la clase, ¿sabéis qué número está justo en medio de 1 y 2? No suelen dudar y dicen que 1 y medio, o 1 y 5 décimas. Entonces pregunto: ¿Sabéis cómo se escribe? Una vez dicho. Entrego a otro niño el cartel con el 1,5 y se coloca dónde considera.
Y, entonces, empezamos a entregar los carteles con el 1,4, el 1,8, el 1,7, el 1,9… Total, que nos hacemos una recta numérica graduada en décimas y queda algo así:
Pero, ¡espera! Cuando miré el 1 por dentro vi décimas y dentro de cada décima vi centésimas entonces:
- ¿De qué manera nombrábamos al 1,2? 1 unidad y 2 décimas.
- ¿Y si tienes que representar 1 unidad y 2 décimas pero no tienes barras? ¡Pues con 20 cubitos!
- ¿Y cómo se llamaban los cubitos si bautizamos a la placa como UNO? ¡Centésima!
- Entonces, ¿cómo se puede llamar también a 1,2? Una unidad y dos décimas o una unidad y 20 centésimas.
¡ALERTA! DEJEMOS DE DECIR QUE EL CERO DE LA DERECHA NO SIRVE! ¿¿¿CÓMO QUE NO SIRVE??? SIRVE PARA COMPRENDER POR QUÉ MOTIVO 1,2 ES TANTO COMO 1,20 Y COMO 1,200.
Bueno, el caso es que si sabemos que al 1,2 también le podemos llamar 1,20 (una unidad y 20 centésima) puedo generalizar y decir que el 1,3 es 1,30 y 1,4 es 1,40…
Y entonces pregunto: oye, ¿y cuál está justo en medio de 1,20 y 1,30? Y sin dudar mucho dicen: «¡1,25!» Y el juego vuelve a empezar. ¿Y sabéis qué? Que nos quedamos pronto sin niños para completar más y más la recta numérica y, aunque nos juntemos con otra clase, con otro curso, con todo el cole, con el barrio, con la ciudad, con el país, con el continente siempre habrá un siguiente al decimal que pongamos.
Horror, el redondeo
Esto del redondeo es un caballo de batalla importante en el cole (da igual con naturales o decimales). Y no me extraña porque, por algún motivo en los libros hablan todo el rato de «si quieres aproximar a la décima te fijas en la cifra de la centésima, si es menor que 5 entonces… y si es mayor que 5 entonces…» Y el pobre niño nunca sabe dónde mirar.
Con lo fácil que sería simplemente esto:
Chicos, tenemos que aproximar el 1,23 a la décima. ¿Os acordáis de la recta de décimas de antes? ¿Os acordáis de que vimos que podríamos pasar toda la vida poniendo niños entre medias?
Y entonces el 1,23 busca su sitio y, él, que ya sabe que puede mirar al microscopio se encuentra con que sabe ubicar el 1,23 sin problema. ¿Por qué? Porque sabe entre 1,2 y 1,3, justo en medio, está el 1,25 así que sabe que el 1,23 está más cerca de 1,2. Y ya.
Tendremos una tercera parte de los decimales en la que abordaremos operaciones, porcentajes…
Continuará…
Para leer el articulo original pincha aquí
Profe Bernabeu