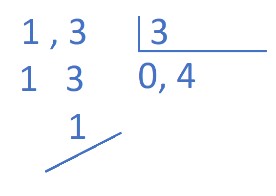Hace unas semanas publiqué una entrada sobre lo importantísimo que era el dominio del número uno (y la poca dedicación que se le presta). En esta entrada nos centraremos nuevamente en el número uno pero esta vez veremos el uno al microscopio, lo veremos por dentro.

Hasta cierta edad, el número 1 es una entidad indivisible para el niño. Uno es uno y ya está, no hay que darle más vueltas. Pero llegado un momento llega a nuestras vidas la necesidad de ver más allá del uno. En realidad, no es mirar más allá, es mirar más adentro. ¿Cuándo ocurre esto? Pues si lo llevamos a la vida cotidiana y con ella al poderoso caballero don Dinero encontramos que hay cosas que valen 1 € y otras que vienen escritas de manera extraña. Por ejemplo, 0,20 €. Realmente no saben cuánto es eso, a qué equivale. Lo que si saben es que con 1 € compran más chuches que con 0,20 €.

Cuando los decimales llegan a la vida escolar del niño (en un curso u otro dependiendo de la comunidad autónoma… Ya sabéis lo diferentes que son los madrileños de los andaluces o los manchegos de los catalanes o lo aragoneses de los asturianos (esto es ironía, claramente)) empiezan a acoger algunos “dejes” que son altamente perjudiciales para la comprensión de este tema y que pueden suponer que el aprendizaje no sea significativo y que no suponga un buen andamio sobre el que seguir construyendo.

Aquí van algunas de las cositas que deberíamos vigilar.

A las cosas por su nombre

Lo principal, como no podía ser de otra forma, es establecer a qué vamos a llamar “uno”.

Si llamamos “uno” a esto:

Sabremos que para representar aquello a lo que llamar “dos”, necesito dos de esos:

Ahora bien, decíamos al inicio del artículo que pondríamos el “uno” al microscopio. Cuando metemos el “uno” al microscopio sin fijarnos demasiado vemos que está dividido en 10 partes iguales. Se ve algo así:

Diez de esas juntas son tanto como “uno”. Pero, ¿qué nombre le podemos dar a cada una de esas partes? Y aquí es dónde viene uno de los problemas típicos en el aprendizaje de los números decimales.

Es frecuente que digamos que cada una de esas se llama “0,1”. Claro, esto incorrecto no es porque no lo es, pero hay un detallito importante que hace que empiecen los problemas. Lo llevaré a un tema más cercano a todos nosotros, el nombre.

  • Hola, ¿cómo te llamas?
  • Me llamo “jota, a, uve, i”

¿Imaginas que la gente dijera así su nombre?

Nunca aterrizamos en los decimales sin haber trabajado previamente fracciones. Si partimos de lo sabido, los niños deberían poder decir que cada una de esas partes se llama “un décimo” o “una décima parte”.

¡Atención! Deberían decir “un décimo”… ¡Pero es que se escribe “1/10”! Cierto, se escribe así pero no hablamos de cómo se escribe sino de cómo se llama. Hablamos de la palabra que designa algo, no del dibujo que utilizamos para representar dicha palabra.

Entonces, dicho esto podemos asegurar que cuando miro el “uno” al microscopio” está formado por “diez décimos” o por “diez décimas”.

Un ejemplito rápido para ver qué importante es llamar a las cosas por su nombre:

Imaginad un problema que se resuelva con la expresión 0,7 + 0,8… ¿Sabéis lo súper habitual que es que un alto porcentaje de niños diga que el resultado es 0,15? Claro, 0 + 0 es 0 y 7 + 8 es 15 así que está claro que 0,7 + 0,8 = 0,15.

Ahora llamemos a las cosas por su nombre:

7 décimas + 8 décimas son 15 décimas. Pude ver al microscopio que 10 décimas hacían una unidad. Así que 7 décimas + 8 décimas son 1 unidad y 5 décimas.

Llegar a la expresión escrita 0,7 + 0,8 = 1,5 será el paso siguiente pero, ¿sabéis qué? Que un niño que entiende, que ha manipulado y descubierto por sus propios medios lee esa expresión así:

“7 décimas + 8 décimas es 1 unidad y 5 décimas”

Y no así:

“cero coma siete + cero coma ocho es uno coma cinco”.

Lo que hay a la derecha de la coma

Demos por hecho que hemos manipulado, que hemos llamado a las cosas por su nombre, que los niños saben que 15 décimas es 1 unidad y 5 décimas y que se escribe así: 1,5.

A mí no me gusta hablar de “trucos” en mates pero reconozco que hay algo que siempre me ha funcionado muy bien para que los niños sepan cuándo y por qué escribir “la coma”.

Imagina que quieres representar con el material anterior la cantidad 1,3. Los niños lo llamarán una unidad y 3 décimas (o 13 décimas).

Cogen una placa como las de arriba. Ya han representado “1”. Cogen otra placa. Habrían representado “2”… ¡Pero no quiero 2! Solo quiero 1,3. ¿Qué hago? Y ellos dicen cosas como “romper una placa” o “cambiar una placa por barras”. Ese “romper un uno” se escribe en matemáticas con una coma.

Sigamos con esta cantidad. ¿Sabemos nombrarla? Sí, de varias formas. ¿Sabemos escribirla? Sí. 1,3

Pues bien. Aquí viene el siguiente error frecuente en el aprendizaje de los decimales. Es eso de “la parte entera y la parte decimal”.

  • Juanito, ¿cuál es la parte entera de 1,3?
  • ¡1!
  • Juanito, ¿y la parte decimal?
  • ¡3!
  • Mira, Juanito: imagina que el material de arriba, el que representa 1,3 fuera de chocolate. ¿Qué preferirías comerte? ¿La parte entera o la parte decimal?
  • ¡La parte entera, claro está!
  • Pero, a ver Juanito. La parte entera dices que es “1” y la parte decimal dices que es “3” y, que yo sepa 1 es menos que 3. Así que, ¿por qué no te comes la parte decimal?
  • Pues porque no es 3, profe. Son tres trocitos, no tres.

Volvemos ooooootra vez a la importancia de llamar a las cosas por su nombre. En 1,3 la parte entera es 1 y la parte decimal es 0,3… ¡No 3!

El error desaparece cuando lo llamamos por su nombre: 1,3 es una unidad y 3 décimas. ¿Qué es más una tableta de chocolate entera o 3 décimas partes de tableta de chocolate?

Otro ejemplito rápido para ver qué importante es llamar a las cosas por su nombre:

Imagina que repartes la cantidad de chocolate de arriba a partes iguales entre 3 amigos. La operación que resuelve eso sería 1,3 : 3. Si nos fuéramos a un algoritmo clásico quedaría algo así:

Mirad, la interpretación de la operación si vemos la representación del chocolate como arriba sería algo así:

Cuando nos repartimos 1,3 tabletas entre tres amigos vemos rápidamente que no tenemos una tableta entera para cada uno. Que hay que romper la tableta. Así que tabletas enteras son cero para cada uno. La coma es eso que indica que hemos tenido que romper la tableta a ver a cuánto tocamos. La cosa es que antes de iniciar el reparto como tal nos encontramos con 13 décimas y al repartírnosla entre los 3 tocamos a 4 décimas cada uno y sobra 1 décima. Es cierto que podríamos seguir repartiendo pero eso lo dejaremos para los contenidos que trabajaremos en el artículo de la próxima semana.

Total que a cada uno nos toca 4 décimas, que se escribe así: 0,4 y sobra… ¿qué sobra?

¿Sabéis qué? Que si han llamado a las cosas por su nombre, no dudarán en decir que sobra 1 décima y se escribe así: 0,1.

Pero si no han llamado a las cosas por su nombre dirán que tocan a 0,4 y sobra 1. ¿Y sabéis qué pasa cuando dicen eso? Que la prueba de la división “no les da” y piensan que la división está mal hecha.

Pues eso, que el dominio del UNO es clave.

Continuará…

Para leer el articulo original pincha aquí

Profe Bernabeu.