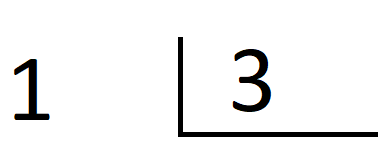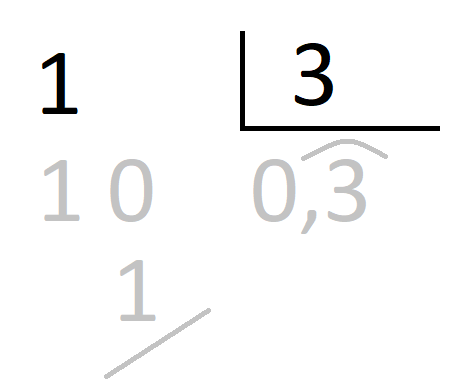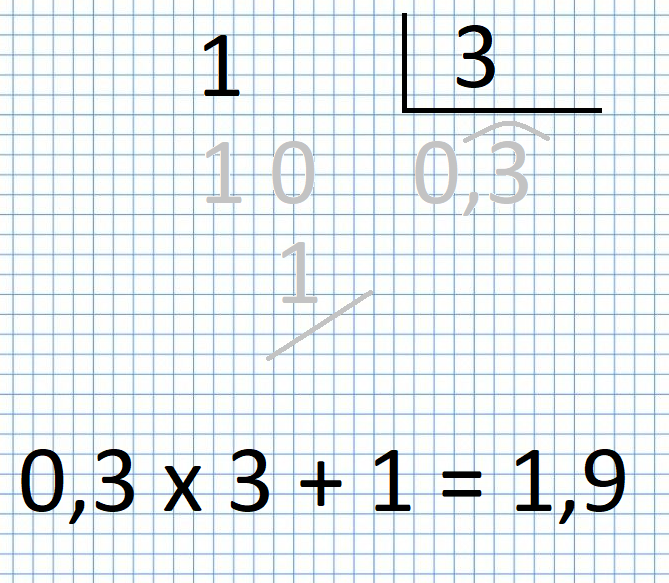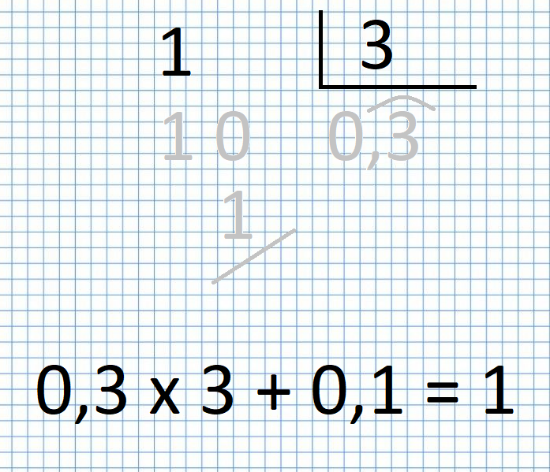DESGRACIADAMENTE EL CÁLCULO ESTÁ DE MODA
En los últimos años se ha puesto de moda algo en infantil y primeros cursos de primaria que, desde mi punto de vista, es muy peligroso. Insisto, bajo mi punto de vista. Que nadie se ofenda pero, cuando en mis formaciones salen las tres siglas famosas de determinado proyecto y me permito opinar (no criticar ni loar, solo opinar), muchos sacan colmillos y garras. Yo no dudo de que la mente del niño está preparada para el cálculo, claro que lo está. De hecho, en general, los humanos, somos buenos en cálculo (aunque las máquinas son mejor).
Esto de que somos buenos en cálculo no lo digo yo, lo dicen los informes PISA. En concreto el 93% de los niños españoles de 14 años son competentes en cálculo. Esto es así antes incluso del surgimiento de los proyectos de tres siglas.
Entonces, si somos buenos en cálculo, ¿por qué demonios hay esa obsesión porque los niños salgan calculando de infantil? ¿Por qué dedicar tanto tiempo a hacer cuentas de 4 sumandos de 5 cifras cada sumando así porque sí? ¿Por qué esas multiplicaciones y divisiones infinitas que da la sensación de que tienen como único objetivo encontrar el error de los niños? ¿Por qué?
¿Sabéis dónde no somos buenos en España (y en muchos otros países entre los que se encuentra… tatatachán…¡Finlandia!)?
En resolución de problemas.
Ahí patinamos. Pero, sin embargo, ¿dónde metemos caña desde que no levantan un palmo del suelo? En cálculo. ¿Por qué? Pues no lo sé, la verdad. ¿Costumbre? ¿Tradición? ¿Quizá porque las matemáticas se asocian a números? ¿Quizá porque el esfuerzo intelectual para resolver problemas es mayor que para resolver cálculos descontextualizados? Seguir un proceso es fácil. Basta con ser ordenado y disciplinado pero resolver problemas es otra historia. Ahí tienes que poner a pleno rendimiento el plato de espaguetis (para los que no sepáis de lo que hablo con los espaguetis os remito a ESTE artículo de hace unas semanas). Ahí hay que tomar decisiones todo el rato y la toma de decisiones suele estar cargada de responsabilidad y asumir responsabilidades es muy muy difícil.
Y entonces, ¿nos olvidamos del cálculo? Pues no. Vayamos construyendo, pero sin prisa.
¿¿¿¡¡¡De qué te sirve que tu niño de 5 años resuelva 37 + 58 si no sabe que en el 37 el “tres” no es tres sino “treinta”!!!??? ¿Sabes que trabajar el “DIEZ” implica saber trabajar en distintas bases de numeración? ¿De verdad consideras que el momento para eso es infantil?
Y digo yo: si como dicen algunos el cálculo es fundamental porque es la herramienta para resolver problemas, ¿quiere decir eso que todos los problemas tienen números? Claramente no. Y si así fuera, ¿es más difícil un problema cuánto más grande son los números? ¿Seguro? No.
En fin, que hay que trabajar los números y los cálculos, claro que sí. Pero siiiiiiin prisa, con tranquilidad. ¿Puedes garantizar que tus niños dominan el “uno”? ¿Seguro?
CON DOMINAR EL UNO SE ACABARÍAN MUCHOS PROBLEMAS EN MATEMÁTICAS
Esto va a sonar exagerado pero… Yo me daría con un canto en los dientes si el dominio del UNO en infantil fuera absoluto y luego ya del 2 en adelante lo trabajaríamos en primaria (¡Oh no! ¡Sacrilegio!). Bueno venga vale, pues hasta el nueve si quieres. Pero con dominio absoluto del uno.
Si domino qué es eso a lo que llamo “UNO” podré saber que a veces tengo UNO y UNO y, a eso, lo llamo “DOS”. Sabré, además, que si tengo “DOS y UNO” necesito encontrar un nuevo nombre para ello y ese nombre es “TRES” y así sucesivamente.
¡Mi hijo de 3 años cuenta de maravilla así que no necesita todo eso! ¿Seguro? Mira:
A ese conjunto de niños lo contaría como: “uno, dos, tres, cuatro, cinco, seis y siete”.
Es más, si le dijeras que escribieran los símbolos que representan esos sonidos (uno, dos, …) haría algo así (quizá invierta algún número):
Y digo yo, si le preguntas a tu hijo o alumno ¿quién es “4”? ¿Respondería que es la niña rubia? Lo digo porque la niña rubia es solo una y no cuatro. Cuatro es el conjunto de 4 niños que representan ese conjunto (empieces por dónde empieces en este caso).
 Si decimos que la niña rubia es la 4 porque es la cuarta, entonces estamos hablando de orden… ¡¡¡¿¿¿Cómo vas a ordenar aquello que no conoces???!!! ¡Pepita ordena! Y la pobre Pepita, que es muy hacendosa, quiere ordenar pero no sabe qué tiene que ordenar.
Si decimos que la niña rubia es la 4 porque es la cuarta, entonces estamos hablando de orden… ¡¡¡¿¿¿Cómo vas a ordenar aquello que no conoces???!!! ¡Pepita ordena! Y la pobre Pepita, que es muy hacendosa, quiere ordenar pero no sabe qué tiene que ordenar.
¿Por qué comenzar ordenando los números sin antes conocerlos? ¿Sabéis qué? Que la mayoría de los niños no saben contar, saben cantar. Cantar una canción que es “uno, dos, tres, cuatro…” pero no saben qué quiere decir cada palabra de esa canción.
Luego llegará el momento en el que veamos que la palabra “cuatro” implica a los 4 elementos del conjunto (no solo a la niña rubia). Pero primero construyamos desde lo conocido:
“Cuatro y uno” recibe un nombre que es “cinco”, que también se puede decir “uno y uno y uno y uno y uno” o “dos y dos y uno” o “tres y dos” o “cuatro y uno”.
Todo este trabajo de composición y descomposición es importantísimo (no en infantil, sino en todas las etapas).
¿Subimos de nivel y vemos porque es importantísimo dominar qué es eso a lo que llamamos uno?
DOMINAR QUÉ ES UNO NO ES SOLO TAREA DE INFANTIL
Vamos a subir a sexto de primaria. ¿Estáis seguros de que vuestros alumnos sabe qué es y qué no es “uno”?
Vamos a ponernos en la siguiente situación. De hecho, profes de 5.º y 6.º, estaría bien que hicierais esta prueba en clase y comprobaseis si esto solo me pasa a mí o en vuestras clases ocurre también. Ponles una división de este tipo:
Entonces harán algo así:
Ok, volvamos a lo de la importancia del dominio del “uno”. Si un niño en sexto NO domina el “uno”, entonces puede darse el siguiente diálogo profe – niño en clase:
Alumno: Profe, ¿está bien?
Profe: Haz la prueba y lo averiguas.
Y aquí está la prueba que ha hecho el alumno:
Y el chaval dice: Pues «no me da», así que está mal. Entonces borra la división y la vuelve a hacer.
¿Y SI DOMINA QUÉ ES ESO DE UNO?
Si el alumno domina qué es eso de “uno” sabrá, de sobra, en este nivel, que para repartir “uno” entre 3, tengo que expresar el 1 como 10 décimas. Así que 10 décimas es otra forma de llamar a uno y le facilita la tarea de reparto. Ahora bien, lo que reparte son décimas y, tras repartir 3 décimas a cada uno sobra 1 décima, que se escribe 0,1 así que la prueba que hará el alumno que domina el “uno” es esta:
Y ya, si el dominio del uno es absoluto verbalizará lo anterior así: “Uno entre tres son tres décimas y sobra una décima”. Y verbalizará la prueba así: “3 décimas por 3 son 9 décimas y más 1 décima son 10 décimas que es 1 unidad.
Ocupémonos en infantil de que los niños dominen el número por dentro, no les metamos mucha caña con números grandes porque, por muy grande que sea el número (N*) que trabajen los niños en infantil (y hasta 4.ºEP) si hay algo que les une a todos ellos es que tiene dentro al UNO.
Caleb Gattegno tiene un libro que lleva por título: “Al fin puede Pepito aprender aritmética”. Hay mucho, mucho, mucho que hacer antes de calcular. Las matemáticas no son números. Que tu niño haga cálculos desde que no levanta un palmo del suelo no quiere decir que razone y no quiere decir que resuelva problemas.
Imagina que tuvieras que elegir solo una de estas dos cosas: Tus alumnos pueden desarrollar el razonamiento lógico y matemático o desarrollar el cálculo. ¿Qué elegirías?
Más razonar, más conectar y menos calcular. Razonar y conectar es específico de los seres humanos.
Be human, my friend.
Para leer el articulo original pincha aquí
Profe Bernabeu