Un cuadrado. Bah, qué tontería. Pues eso, un cuadrado es un cuadrado y ya está. Punto y final.

Bueno, tengo que decir que “un día” (fueron meses) me tomé la molestia de averiguar en qué medida era importante dominar la forma cuadrada para la consecución de otros objetivos. No hablo solo de geometría. Hablo de objetivos relacionados con todos los bloques de contenido del currículo (numeración, cálculo, medida, geometría, lógica, probabilidad y estadística). Por supuesto, todo trabajado desde la resolución de problemas.

Total, que puse por escrito todos los contenidos de matemáticas de infantil y primaria y pude comprobar que, en alrededor del 65% de ellos, es necesario dominar la forma cuadrada.

En 5 líneas ha aparecido en 2 ocasiones el verbo dominar. No hablo de identificar, de discriminar, de clasificar, de seriar, de averiguar su área o su perímetro, no. Hablo de dominar el cuadrado y sus propiedades en toda su extensión. ¿Sabéis qué? Que del cuadrado hay que saber mucho más que eso de los 4 lados iguales y 4 ángulos rectos. Pero mucho, mucho más.

Materiales para el taller

No entraré en este artículo en todo en lo que se ve envuelto el cuadrado. Solo voy a proponer un problemita que me encanta y que suele ser polémico en las formaciones con profes de infantil y primaria y que suele generar unas discusiones y razonamientos tan tan bonitos que merece la pena compartirlos por aquí.

Pero si hay algo bonito es ver a los niños rompiéndose la cabeza tratando de encontrar el motivo y descubriendo, al final, porque las abejitas son tan listas y bonitas.

Todo esto es lo necesario para poder hacer este taller en clase o en casa y que los niños se queden con la boca muy abierta como diciendo: IM PO SI BLE. NO PUEDE SER. ALGO FALLA. Pero no, no falla nada, son solo matemáticas y las matemáticas no fallan:

  • Un ovillo de lana.
  • Un taco de pósit cuadrados de 7,5 cm de lado (los estándar).
  • Cinta métrica o regla de 1 metro.
  • Cinta adhesiva.
  • Tijeras.
  • ¾ de hora.
  • Niños.
  • Profes (o padres) preguntones.

Mide, corta, ata

 

Mide con la regla un trozo de lana de 92 cm. Ahora, anúdalo por los extremos de esta forma::

Realmente necesitamos 92 cm porque 2 cm aproximadamente es lo que sobra al hacer el nudo. La idea es que la parte anudada mida 90 cm aproximadamente. Es lana, será difícil hacerlo muy exactito pero para lo que queremos hacer valdrá con una buena aproximación.

Formando cuadrados y rectángulos

Haced una forma cuadrada. Mirad podéis hacerlo así:

Poneos por parejas y meted los dedos índice de cada mano (el índice es el de señalar) en el interior del trozo de lana, tu compañero hará lo mismo.¿Podéis hacer una forma cuadrada? Para poder llamarlo cuadrado necesitamos cubrir la superficie. Podéis pegarlo en el suelo o en la pared o en la pizarra utilizando cinta adhesiva.

Como sois dos y habéis utilizado un trozo de lana, os sobra otro. Con ese otro trozo haced una forma rectangular y pegadla para llenarla de superficie. Pegadla junto al cuadrado. Luego necesitaremos que el rectángulo tenga unas determinadas medidas. De momento es suficiente con que tenga forma de rectángulo y esté pegado junto al cuadrado. Mira, algo así:

Empezamos con retos sencillitos

Recuerda que el trozo “útil” de lana mide 90 cm. Sabiendo esa información, ¿puedes averiguar el lado del cuadrado? ¿Fácil? Sí, ¿verdad?

¿Cóóóóóóóóómo? ¿Quééééééé? ¿Te resulta complicado hacer 90 : 4? (Nota mental, hacer una entrada sobre cómo dividir fácilmente).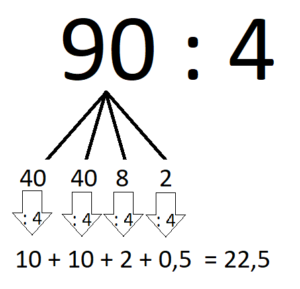

¡Qué difícil! Ok, pues hazlo con cajita. Da igual, en esta entrada estamos a otra cosa. 😊

Bueno, el caso es que si la lana mide 90 cm, cada lado mide 22,5 cm. O lo que es lo mismo, si el perímetro del cuadrado es 90 cm, el lado mide 22,5 cm.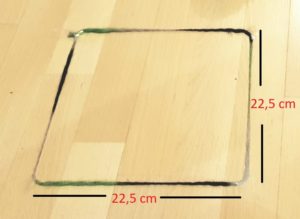Ahora vamos a por el rectángulo. Si el trozo de lana mide 90 cm, ¿cuánto mide el lado? ¡Hay muchas opciones! A ver, cuáles, cuántas, a ver cuántas sacamos entre todos. Es un poco de cálculo mental camuflado.

Bueno, según quieras el rectángulo más o menos “armónico” elegirás una medida u otra. A mí me gustan mucho los rectángulos que son el doble de largo que de ancho (aunque me gustan más los áureos (nota mental, posible entrada sobre el número de oro y la divina proporción). Así que: “¡Niños, queremos conseguir que el rectángulo sea el doble de largo que de ancho!” Y aquí está el nuevo reto. No tardan mucho en llegar a la conclusión de que el rectángulo debe medir 30 cm de largo y 15 cm de ancho.

Un reto obvio pero necesario

Ya tenemos un cuadrado pegado en el suelo. Ya tenemos un rectángulo pegado en el suelo. El reto obvio pero necesario es:

¿En cuál de las dos figuras has utilizado más lana? ¡Qué tontería, por favor! ¡Pues la misma!

Pues claro, si has utilizado 90 cm de lana para el cuadrado y 90 cm de lana para el rectángulo es como si me preguntas que de qué color es el caballo blanco de Santiago.

El rectángulo de lana y el cuadrado de lana está pegado en el suelo, ¿verdad?

Otro reto “obvio” pero necesario: ¿Hay más cantidad de suelo dentro del cuadrado o dentro del rectángulo? ¡Profe qué tontería! Pues igual…

¿Y eso por qué? ¡Pues porque hemos usado la misma cantidad de lana en ambos casos!

El maravilloso invento de los pósit cuadrados

El siguiente reto es tan sencillo como sorprendente. Coge tus pósit y rellena ambas figuras. Si, como tú dices hay la misma cantidad de suelo en el rectángulo y en el cuadrado entonces, deben caber los mismos pósit en el cuadrado y en el rectángulo pero…

¡ESPERA UN MOMENTOOOOOOOOOOOOOOOOOO! ¿QUÉÉÉÉÉÉÉ? ¿CÓÓÓÓÓÓÓMO?

Vamos con las formulitas

Los pósit han demostrado que a igual perímetro no siempre se cumple que tengamos igual área. Si no termina de convencerte es porque tu mente abstracta de señor o señora mayor te obliga a aplicar formulitas para creértelo.

Mira, estas eran tus figuras y sus medidas. Así que sus áreas deben ser estas:

Recuerda: Área del cuadrado = lado x lado

Recuerda: Área del rectángulo = base x altura

Entonces llegan las abejitas

¿Y por qué no decidieron hacer sus panales con celdas cuadradas? ¡Pues porque aprovechan mejor con hexágonos! ¿Y sabes por qué? Porque gastan menos cera para conseguir hacer celdas más grandes si lo hacen en forma hexagonal que en cuadrada.

Si el perímetro es 90 cm, ¿cómo puedes calcular el lado del hexágono regular? ¡Pues 90 : 6!

¡Qué difícil! No, mira, 90 es 60 y 30 y 60 : 6 es 10 y 30 : 6 es 5. Así que 90 : 6 es 10 y 5 que es 15 (no olvidar la nota mental de la división).

Así que el lado del hexágono es 15 cm. Para calcular el área del hexágono puedo hacer varias cosas.

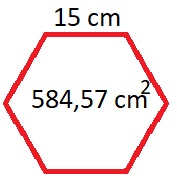Los mayores hacen esto: (Perímetro x apotema):2. Para calcular la apotema podríamos aplicar Pitágoras (nota mental, entrada sobre Pitágoras… ¡Ah no, esa ya está!).

Total que no haremos el desarrollo pero tenéis que saber que el área del hexágono regular de 15 cm de lado es 584,57 cm2. ¡Qué es mayor que la del cuadrado!

¡Pues para eso que hubieran elegido la forma circular porque el área de un círculo de 90 cm de longitud de circunferencia (de perímetro) es 644,22 cm2!

¿Y por qué no lo hicieron? ¡Pues porque el círculo no tesela el plano y esos huequecillos entre celda y celda son una faena!

Mira qué son listas estas abejillas. Seguramente es mi bichito favorito (después del bicho bola).

¡VIVAN LAS ABEJAS! ¡Y VIVA LA MIEL!

 

Para leer el articulo original pincha aquí

Profe Bernabeu.